Stresses At Elliptical Holes

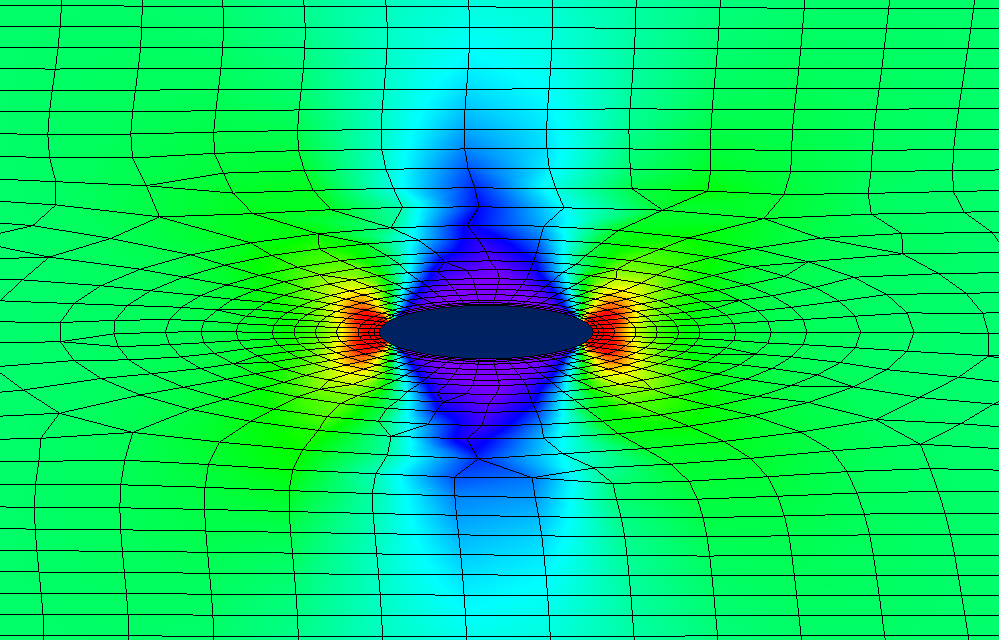
Introduction

Charles E. Inglis's linear elastic solution in 1913 for the stress field surrounding an ellipse is the next major step in the development of Linear Elastic Fracture Mechanics (LEFM) Theory [1]. Like Kirsch's solution for the circular hole [2], it applies to an infinite isotropic plate in uniaxial tension. Unlike Kirsch's solution, it is applicable to an infinite number of different scenarios corresponding to ellipses having different aspect ratios. And in the limit, it applies to an ellipse flattened to form a crack.

Like the situation of the circular hole, the mathematical derivation of the stress field around the ellipse will not be reviewed here because there is nothing to be learned from it (and it is torturous to work through). Inglis's original paper covering all the steps can be viewed here. Instead, we will only present the key results. However, the Elliptical Coordinates that Inglis used to solve the problem will be discussed because they are quite interesting.

Elliptical Coordinates

Elliptical coordinates are a generalization of 2-D polar coordinates that are ideally suited to problems involving ellipses, just as polar coordinates are ideally suited to problems involving circles. They are defined by the following equations

\[ \begin{eqnarray} x & = & c \cosh (\alpha) \cos (\beta) \\ \\ y & = & c \sinh (\alpha) \sin (\beta) \\ \end{eqnarray} \]
that relate \((x,y)\) to \((c,\beta)\) with \(\alpha\) being a fixed parameter based on the aspect ratio of the ellipse.

One can confirm that this is an ellipse by expressing \(\cos^2 \beta + \sin^2 \beta = 1\) in terms of the above equations. This gives

\[ \left( x \over c \cosh (\alpha) \right)^2 + \left( y \over c \sinh (\alpha) \right)^2 = 1 \]
which is an ellipse with major axis equal to \(c \cosh (\alpha)\) and minor axis equal to \(c \sinh (\alpha)\).

At very small \(\alpha\)'s, the ellipse approaches a crack. At infinitely large \(\alpha\)'s, \(\cosh (\alpha)\) and \(\sinh (\alpha)\) approach each other, permitting both \(c \cosh (\alpha)\) and \(c \sinh (\alpha)\) to be replaced by \(r\), and the elliptical coordinates become classical polar coordinates.

The figure below shows two examples of elliptical coordinates, the left with a small value of \(\alpha\), and the right with a large value of \(\alpha\).

The \(\alpha\) parameter can be determined from the ratio of the max and min axes of the ellipse. An ellipse with width, \(2a\), and height, \(2b\), has an \(\alpha\) value determined by

\[ {2 \, b \over 2 \, a} \; = \; {2 \, c \sinh (\alpha) \over 2 \, c \cosh (\alpha)} \; = \; \tanh (\alpha) \]
So taking the inverse hyperbolic tangent of \(b / a\) gives \(\alpha\).

And setting \(\alpha\) to a very small number flattens the ellipse to form a crack.

Note that it is common to use \(a\) and \(b\) to represent the major and minor axes of ellipses. Therefore, \(a = c \cosh (\alpha)\) and \(b = c \sinh (\alpha)\).

Hyperbolic Functions

Here's a quick review of hyperbolic functions.

\[ \sinh(x) = {e^x - e^{-x} \over 2} \qquad \qquad \cosh(x) = {e^x + e^{-x} \over 2} \qquad \qquad \tanh(x) = {\sinh(x) \over \cosh(x) } \]

Stresses at Elliptical Holes - Inglis's Solution (1913)

Not only did Inglis use elliptical coordinates to solve the elliptical hole problem, but he also used complex numbers. The bottom line is that the derivation is endlessly painful math that provides no physical insight. Not to minimize what Inglis accomplished; it is a great achievement. But all we need are the results.

And the results are surprisingly straight forward. The maximum stress at the tip of the ellipse is related to its size and shape by

\[ \sigma_\text{max} = \sigma_\infty \left( 1 + 2 {a \over b } \right) \]
It is clear that Inglis's elliptical result reduces to the familiar \(\sigma_\text{max} = 3 \, \sigma_\infty\) for the special case of a hole when \(a = b\). On the other hand, the max stress is predicted to go to infinity as the ellipse flattens to form a crack (\(b \rightarrow 0\)).

The radius of curvature, \(\rho\), at the tip of an ellipse is related to its length and width by

\[ \rho = {b^2 \over a} \]
Solving this for \(b\) and substituting into the \(a/b\) ratio in \(\sigma_\text{max} = \sigma_\infty (1 + 2 a / b )\) gives

\[ \sigma_\text{max} = \sigma_\infty \left( 1 + 2 \sqrt{ a \over \rho} \right) \]
This is considered the more fundamental result because it relates the maximum stress at the tip of the ellipse to parameters there: (i) the distance to the tip, \(a\), and (ii) the radius of curvature at the tip, \(\rho\).

Radius of Curvature, \(\rho\)

The radius of curvature of the ellipse tip can be found by first solving the ellipse equation for \(y\)

\[ y = b \, \sqrt{1 - \left(x \over a \right)^2} \]
Next, substitute this into the equation for radius of curvature

\[ {1 \over \rho} = { y'' \over \left[ 1 + \left( y' \right)^2 \right]^{3/2} } \]
and evaluate the result at \(x = a\)

\[ \rho = {b^2 \over a} \]

Inglis's solution with the square root function is landmark for two reason. First, it shows that as the radius of curvature at the tip goes to zero (the definition of a crack!), the stress there goes to infinity, even for the slightest remote load. Of course, stresses in the real world can't exceed a material's yield strength. Nevertheless, a common trait of Linear Elastic Fracture Mechanics (LEFM) theory is that stresses at crack tips are predicted to be infinite.

The second landmark result is that the stress at the tip is proportional to the square root of the ellipse's width, even in an infinite-width plate. This is also consistent with LEFM theory. And it is obviously different from the stress state at a circular whole, which is independent of the hole's size.

Relevance of an Infinite Stress Prediction

Inglis's solution evidently spurred much debate because of its prediction of infinite stress at a crack tip. Its relevance was questioned because stresses can never in fact be infinite, but are instead limited by a material's yield or failure strength. Nevertheless, Inglis's result is completely correct for the problem he proposed, which was linear elastic, meaning that the material behavior is governed by Hooke's Law and has no limiting yield/failure stress.

One might ask, "Why bother solving a problem with an infinite yield stress that can't possibly exist in the real world?" The answer is simple. Inglis solved this problem because it was the only one that could be solved. Incorporating a finite yield stress would make the problem nonlinear and impossible to solve analytically. And in fact, his analytical solution quickly proved to be extremely valuable to furthering the understanding of crack behavior because Griffith used it to develop his energy-based failure criterion.

The difference in hole/ellipse size sensitivity can be related back to the force flow field concept discussed on the previous page on circular holes. It was said that the height of a circular hole, being equal to its width, gives the force flow-field advanced warning of the upcoming diversion. In contrast, an ellipse of equal width will not be as tall as the circular hole and will not give the flow-field as much warning. This leads to higher stress concentrations. The limit of this trend is the crack, which has zero radius and produces an infinite stress concentration at its tip.

I wonder how long it takes to recognize the significance of key technological contributions. In Inglis's case, it could have been decades. Nevertheless, it is clear today that he, through his analytical solution for the ellipse, was the first to demonstrate that the stress concentration is proportional to \(\sqrt{a}\) and that it goes to infinity as the ellipse squashes down to form a crack.

Today, these properties are taken for granted as foundational aspects of Fracture Mechanics. Even at Inglis's time, it was known that small cracks could cause glass panes to shatter. Inglis mentions this in his 1913 paper, and notes that his solution explains the high stress levels responsible for the shattered panes.

One more historical diversion, concerning another major achievement that occurred in 1913. In that year, Richard von Mises published his famous von Mises yield criterion, applicable to isotropic ductile metals. So 1913 was a very good year! More information on the von Mises stress and yield criterion can be found here: www.continuummechanics.org/cm/vonmisesstress.html.

References

Inglis, C.E., "Stresses in Plates Due to the Presence of Cracks and Sharp Corners," Transactions of the Institute of Naval Architects, Vol. 55, pp. 219-241, 1913.
Kirsch, E.G., "Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre," Zeitschrift des Vereines deutscher Ingenieure, Vol. 42, pp. 797-807, 1898.

Acknowledgements

Thanks to Greg Todd for contributing to this page.